モチベがあるうちに駆け抜けておきたい。
第1問 難易度:D****

これは厳密には初見ではなく、僕が高3の頃に場合の数の基本を忘れないために個別に取り組んでいた問題です。10分で終わったから1回しか解いてないけど。
いかにも場合の数の基本を集めましたみたいな問題で、標準参考書の例題に載っていても違和感がない見た目をしています。
場合の数の数え上げにおいてはものを区別する、しないが重要だと普段から耳が痛くなるほど聞かされているでしょうが、まさにその基本がちゃんとできているかを試してくるある意味で東大らしい問題と言えるでしょう。
で、そんなめっちゃ基本的なことを問われているはずなのに、難易度がDと書かれているのは数学教育の敗北か???
(1) 3^n
(2) ボールの区別がつかない場合、それぞれのハコに入っている個数だけを考えることになりますから

このように、ボールを1列に並べておいて、その間にどのハコに入れるかを表す仕切りを挿入すると考える、という考え方をするのでした。いわゆる重複組み合わせです。
これはn個のボールと2個の仕切りの並べ方になるから、(n+2)_C_2通りとなります。
正直東大とか関係なく、ここまではできてもらわないと結構困ります。間違えた人は教科書の勉強でもしておいてください。
(3)
ハコに区別が無い場合、とりあえず区別して入れたとしておいて、あとから重複度で割るのが基本でした。
例えば
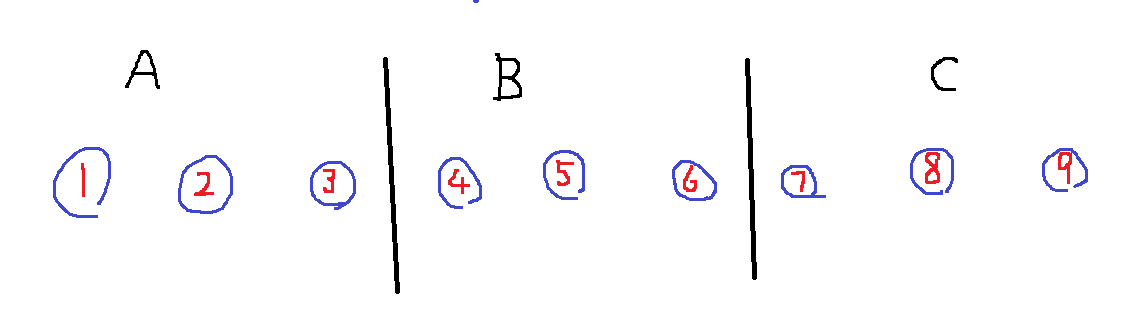

上の2つの場合は、ハコにA,B,Cという名前がついていたら別の入れ方になりますが、ハコから名前が無くなると同じ入れ方になるのです。
ハコの名前の付け方は6通りあるため、答えは3^n/6通りだ!
はい。そんなわけないですね。そもそもこれ整数じゃないので間違ってるに決まっています。
というのも名前がついていてもなお区別できない状況というのが存在するのです。それは1個のハコに全てのボールが入っている場合です。

これは、BとCを入れ替えた場合を考えると、ハコに名前がついていようが同じ入れ方ですね。ということはこの3通りについては (Aに全部、Bに全部、Cに全部の3通り) 別枠で考えてやる必要があります。
全入れが1通りに圧縮されて、それ以外の3^n-3通りは1/6に圧縮されるため、答えは(3^n+3)/6通りです。
(4)
なんでここに来てnが6の倍数という制約がついているのかというと、これはどうも一般のnについて場合の数を求めることができないかららしいです。
ボールにもハコにも区別が無いので、個数の組み合わせが何通りあるかを考えます。(3)と同じようにハコに区別があるとしてから後から区別を取っ払ってやるというようにするのですが、例えばボールが12個あるとして
(3個、4個、5個) → 名前の付け方は6通り
(3個、3個、6個) → 名前の付け方は3通り
(4個、4個、4個) → 名前の付け方は1通り
と、同じ個数のハコが何個あるかによって名前の付け方が何通りあるかが変わってくるので結構厄介です。
それでは各場合について何通りあるかを見ていきましょうか。
(i) 3箱とも同じ数。
(2m、2m、2m) だけなので1通り。ハコに区別があるとしても同じです。
(ii) 3箱中2箱が同じ数
(0、0、6m)、(1、1、6m-2)、……、(3m、3m、0) の3m+1通りがあるはずです! …と言いたいところですが途中で(2m、2m、2m)を通過するのをうっかり忘れてしまいがちです。というわけで3m通り。ハコに区別があるとするならば9m通りですね。
(iii) 3箱とも数が違う
これは直接考えるには難しすぎます。ここでハコを区別した場合の(2)の答えを拝借して余事象を考えます。(i)、(ii)はハコに区別があるとしたならば合計9m+1通りで、また(2)の答えはn=6mに置き換えたら(3m+1)(6m+1)通りとなります。
このことから、3箱とも数が違う場合はハコの区別があるとしたとき(3m+1)(6m+1)-(9m+1)=18m^2通りとなるはずです。
ならば区別をなくすと3m^2通りになりますね。
というわけで答えは3m^2+3m+1通りで、n=6mを使って書き換えると(n^2+6n+12)/12通りとなります。

第2問 難易度:D***

かかった時間:76分20秒
等面四面体は直方体に埋め込めというマニアック定石を知っていれば10分で終わります。が、あまりにも受験技巧が過ぎるのでこれを知らないものとして解くとどうなるか? というのを今回はやってみました。
(1)
とりあえず四面体を組み立てて、線分PQはここの長さです。

こんなものは万能計量ツール「ベクトル」を使えばなんとかなるというのは高校2年生くらいの頃から耳が痛くなるほど言われていることです。
3辺をそれぞれ1次独立な3つの基本ベクトルとして設定して、内積は余弦定理から求まるので…

はいできた。
(2)
正直僕がベクトル苦手で外積がどうとかよくわからないので、原始的な方法である「底面積×高さ÷3」に頼ることにします。

恐らく(1)は誘導だと思うので、三角形PBCを作って四面体の体積を二等分し、高さを頑張って出すことにします。ちなみに内積計算によりBC⊥PQがわかるため、底面積は簡単に求まるはず。
OP⊥PQなので高さはa/2だろ! と思った人は不正解です。高さというのは点Oから平面PBCに下ろした垂線の長さのことを指し、点Oから直線PQに下ろした垂線の長さではないからです。一緒じゃないの? という人は下図参照。

というわけで三次元ってのはなかなか厄介なのです。困りましたね。
それでは垂線の長さをどうやって求めればいいのか? とりあえず足をHとおくと、ここで受験数学使わないランキング1位の無名定理「三垂線の定理」からHP⊥PQが分かります。マジで初めて使ったわこんな定理。そして平面PBC上にあってPQに垂直な直線として既に直線BCがあるため、BC//HPがわかります。ということは…?
OH↑=OP↑+tBC↑
なる実数tが存在することを意味します!
tを決定するためには、垂直条件を適当に持ってくればよいでしょう。平面PBC上のベクトルならなんでもいいです。一番簡単そうなのがBC↑っぽいのでそれで。

tが求まれば、高さも求まります。

ここまで終われば体積が求まりますが、正直言ってめちゃくちゃ疲れました…。簡単にやってそうですが、すぐ思いつく方法は未知数が2個以上あって死ぬほど面倒だったので、未知数を1個にして計算を楽にする工夫 (三垂線の定理の利用) を思いつくまでに1時間以上かかってます。
ここから得られる教訓は以下。
等面四面体は直方体に埋め込める ←覚えろ!!

第3問 難易度:C***

かかった時間:21分35秒
まさかの微分方程式。この時代は学習指導要領にあったらしい。
指定暴力団鉄緑会でも一応微分方程式はやったんだけど、やってることの意味が全く分からなくてこの回の復習テストが6点だったのは覚えています。100点満点です。ゴミ。

問題文に書かれていることをそのまままとめるとこうです。高3当時の僕だと恐らくここから何がどのパラメータに依存して変化するのかっていうのが分からずに手も足も出ないと思います。
だって、それまで例えばxに依存する関数は「f(x)」などという形でxに依存しますよということが明示されてきたのに、いきなり「Vはhに依存します」って言われてもわからんわっていう感じです。こんなんでも鉄緑SA行けるんやな。
これだとまだ微分方程式を立てたといえませんから、Vとhの間の関係式を導いてやります。
ところで石油タンクのサイズ感すら与えられてないので勝手に底面の半径r、高さLとでも置いておいて、断面積は2L√(2hr-h^2)になる。当然これは体積Vを微分したものであるため、dV/dt=2L√(2hr-h^2)・dh/dtが成り立ちます。
つまり微分方程式はこうなる。

移行してこんな感じ

両辺積分して

初期条件 (って言うんかなこの場合) として、t=0のときにh=2r、t=60 (分) のときにh=rとなると言われているため、C=0、k=-Lr^(3/2)/45と出てきます。
あとは、h=0になるtを具体的に求めてやると、t=120√2と出てきます。
60分後からの経過時間が問われているので、120√2-60の整数部分である109分 (1時間49分) が答えとなります。
これが難しいのかどうかはぶっちゃけ知らない。
